Constraint satisfaction is divided into two stages: planning and run-time. Planning commences when a object is presented with a message plan. This message plan is not an actual request to do something; rather, it is a declaration of intent – a description of a message that might be sent to the object. Given this description, the object will generate a plan to be used at run-time for receiving such messages, while satisfying any constraints that might be affected. The results of this planning are compiled as a Smalltalk method. Directions for calling the compiled method are returned as a new message plan.

Consider the quadrilateral example described in Chapter 2 (shown again in Figure 5.1).

Figure 5.1 – Moving the vertex of a quadrilateral

When the user select move Point and first positions the cursor over a vertex of the quadrilateral, the ThingLab window composes a message plan and present it to the quadrilateral. The quadrilateral decides how to move its vertex while still keeping all the midpoint constraints satisfied, and embeds this plan in a compiled Smalltalk method. It then returns another message plan that gives directions for invoking that method. As the user pulls on the vertex wit the cursor, the window repeatedly sends the quadrilateral a message asking it to update its position. This message invoke the Smalltalk method that was just compiled.

During planning, the object that presented with the message plan creates an instance of ConstraintSatisfier to handle all the work. The constraint satisfier gathers up all the constraints that might be affected by the change, and plans a method for satisfying them. The constraint satisfier will first attempt to find a one-pass ordering for satisfying the constraints. There are two techniques available for doing this: propagation of degrees of freedom, and propagation of known states. If there are constraints that cannot be handled by either of these techniques, the constraint satisfier will ask the object for a method for dealing with circularity. Currently, relaxation is the only such method available. If relaxation is used, the user will be warned, so that perhaps some other redundant constraints can be supplied that will eliminate the need for relaxation.

The constraint satisfaction methods used in ThingLab will now be described in more detail. To illustrate the operation of the methods, the electrical circuit example form Chapter 2 will be used. [See that chapter for descriptions of the parts involved. Additional labels have been added to the picture in Figure 5.2 to make it easier to refer to the various parts.]

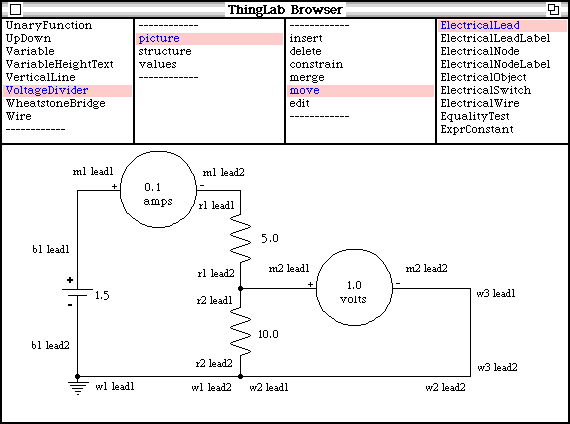
Figure 5.2 – A voltage divider

In propagating degrees of freedom, the constraint satisfier looks for a part with enough degrees of freedom so that it can be altered to satisfy all its constraints. If such a part is found, that part and all the constraints that apply to it can be removed from further consideration. Once this is done, another part may acquire enough degrees of freedom to satisfy all its constraints. The process continues in this manner until either all constraints have been taken care of, or until no more degrees of freedom can be propagated.

Because of the difficulty of giving a precise definition of degrees of freedom for non-numeric objects, the current constraint satisfier uses a simple-minded criterion for deciding if a part has enough degrees of freedom to satisfy its constraints: it has enough degrees of freedom if there is only one constraint that affects it. It doesn’t matter whether or not the constraint determines the part’s state uniquely (removes all its degrees of freedom). [the power of the method could be increased by taking advantage of the cases where better descriptions can be given of the degrees of freedom available to a part]

In deciding when a constraint affects a part, the part-whole hierarchy must be taken into account. The set of constraints that affect a given part is found by checking whether the path to the part overlaps the paths of any of the message plans generated by the constraints. Thus, a constraint on the first endpoint of a line affects the line as a whole, the first endpoint, and the x coordinate of the first endpoint; but it doesn’t affect the line’s second endpoint.

In the voltage divider example, the text that displays the voltmeter’s reading has only a single constraint on it: that it correspond to the voltage drop between m2 lead1 node and m2 lead2 node. Similarly, the text in the ammeter is constrained only by its relation to m1 lead1 current. Therefore, these pieces of text can be updated after the voltage drop and current are determined, and their constraints can be removed from further consideration. In this case, there are no propagations that follow.

This method is very similar to the previous one. In propagating known states, the constraint satisfier looks for parts whose state will be completely known at run-time, i.e., parts that have no degrees of freedom. If such a part is found the constraint satisfier will look for one-step deductions that will allow the states of other parts to be known at run-time, and so on recursively. For the state of part A to be known (in one step) from the state of part B, there must be a constraint that connects A and B and that determines A’s state uniquely. This is indicated by the uniqueState flag on the message plan whose target is A. When propagating known states, the constraint satisfier can use information from different levels in the part-whole hierarchy: if the state of an object is known, the states of all its parts are known; if the states of all the parts of an object are known, the state of the object is known.

If the state of a part is uniquely determined by several different constraints, one of the constraints will be used to find its state, and run-time checks will be compiled to see if the other constraints are satisfied.

In the example, this method would be used as follows. By the constraint on the ground, at run-time b1 lead2 node voltage will be know. [Actually, it is already known during planning, but the constraint satisfier doesn’t use this information.] Also, by the battery’s constraint b1 lead1 node voltage will be known, which is the same as m1 lead1 node voltage. The ammeter has a constraint that there be no voltage drop across it, and so m1 lead2 node voltage will be known. Similarly, the voltmeter has a constraint that it draw no current, and so the current in its leads and connecting wires will be known. Finally, by the constraint on the wires, w1 lead2 node voltage, w2 lead2 node voltage, and w3 lead1 node voltage are all known.

The voltage at the node between the resistors, and all the other currents, are still unknown.

If there are constraints that cannot be handled by either of these techniques, the constraint satisfier will ask the object for a method for dealing with circularity. Currently, relaxation is the only such method available (unless the user supplies more information – see below). Relaxation can be used only with objects that have all numeric values; also, the constraints must be such that they can be adequately approximated by a linear equation.

When relaxation is to be used, a call on an instance of Relaxer is compiled. At run-time, the relaxer changes each of the object’s numerical values in turn so as to minimize the error expressions of its constraints. These changes are determined by approximating the constraints on a given value as a set of linear equation are calculated by noting the initial error, and by numerically finding the derivative of the error expressions with respect to the value. Relaxation continues until all the constraints are satisfied (all the errors are less than some cutoff), or until the system decides that it cannot satisfy the constraints (the error fail to decrease after an iteration). [See Sutherland 1963 for a fuller description of the relaxation method.]

Often, many more parts would be relaxed than need to be. To help ease this situation, a trick is used during planning. The trick is to try assuming that the state of one of the parts to be relaxed, say P, is known. This part P is chosen by looking for the part with the largest number of constraints connecting it to other still unknown parts. P is placed in a set S. Then the method of propagation of known states is invoked to see if the states of any other parts would become known as a result. All the parts which would become known, along with P itself, are eliminated from the set of parts to be relaxed. The process is repeated until the set of parts to be relaxed is empty. At run-time, only the parts in S are relaxed. As each part P in S is relaxed, the system also computes the new states of the parts which had become known as a result of assuming that P was known. In computing the error in satisfying the constraints on P, the system considers the errors in satisfying both the constraints on P itself, and also these other parts. [The heuristic for choosing P was adapted form tha used in the EL circuit analysis program for picking an unknown when doing symbolic algebraic manipulations (Stallman & Sussman 1977)].

In the voltage divider, r2 lead1 current has tree constraints connecting it to other unknowns: the Ohm's law constraint on r2, r2's constraint inherited from TwoLeadedObject and the Kirchoff's law constraint on r2 lead1 node. No other unknown has more constraints, and so the system will try assuming that it is known. Given its value, r2 lead1 node voltage and all the other currents would be known. Therefore, at run-time, only r2 lead1 current will be relaxed.

Using the method employed by Steele and Sussman [Steele & Sussman 1978], another view of the voltage divider may be added that obviates the need for relaxation. First, a new class is defined that embodies the fact that two resistors in series are equivalent to a single resistor.

The constraint specifies that the resistance of the equivalent single resistor be equal to the sum of the resistors in series. The first merge simply connects rA and rB in series. The other merges, however, apply to leads rather than nodes. The second merge states that rA lead1 and rSeries lead1 are identical. Hence, the currents in these leads are also identical and rA lead1 node will have a single current flowing into it. [All this is handled automatically by the system -- all the user needs to do is enter the merge.] The third merge plays an analogous role.

In the picture of an instance of SerieResistors (Figure 5.3), the symbol for rSeries is offset to the left and connected with dotted lines, indicating that it is an equivalent circuit element rather than a resistor in parallel with rA and rB.

Figure 5.3 - Picture of the prototype SeriesResistors

The resistors rA and rB of SeriesResistors are designated as attachers. To add this new description to the voltage divider an instance of SeriesResistors is inserted in the circuit (call it series), and the resistors rA and rB of series are merged with the existing resistors r1 and r2 in the circuit (Figure 5.4).

Figure 5.4 - The voltage divider with an added instance of SeriesResistors

Using this additional description, all the constraints can be satisfied in one pass. As previously described, m1 lead2 node voltage and w1 lead2 node voltage are both known. These are the same as series rSeries lead1 node voltage and series rSeries lead2 node voltage respectively. Thus, by the Ohm's law constraint on series rSeries, series rSeries lead1 current is known. But this is the same current as series rA lead1 current, and also the same as r1 lead1 current. Again by Ohm's law, the voltage at the midpoint, r1 lead2 node voltage, is known. All the other currents are also known.

There are many questions remaining to be explored in connection with the use of multiple views in constraint satisfaction. [See also Chapter 6.] For example, one should be able to tell the system explicity about redundant views. This would allow the system to use propagation of degrees of freedom in the presence of such views, and would also allow it to do some cheching to see that it was appropriate to apply te redundant view.

In the above example, propagation of degrees of freedom was used to postpone updating the ammeter's reading until after the voltages and currents had been found. However, suppose tht there were another constraint on the ammeter that gave a redundant description of how to update the next that displays its reading. In this case, the system would not have been able to use propagation of degrees of freedom, since it would not know that a value for the text could always be found that would satisfy both constraints simultaneously. If these two constraints were explicitlydescribed as being redundant descriptions, however, the method could still be used.

In regard to checking whether it is appropriate to apply a redundant view, consider the process described above of viewing two resistors in series as being equivalent to a single resistor. The parts rA and rB of an instance of SerieResistors should only be merged with a pair of resistors that are already connected, and there should be no significant other current flowing from the center node of the resistors. In one sense, the system already connected, the act of merging the two resistors from an instance of SerieResistors will cause them no be connected. Also, if there is a significant will be satisfied at run-time. However, the system could do a better job of informing the user of unsatisfiable constraints if it knew about the use of a redundant description.

During planning, an object is presented with a message plan that describes a Smalltalk message that might be sent to it at run-time. The object constructs a method for receiving such message, and returns a new message plan that gives directions for invoking the method. This is called transforming the message plan. In the simple case, when no constraints are present, the result of transforming the message plan is the same as the original plan. However, a quite different plan may be returned if there are constraints that would affected by the message described by the original plan.

As a simple example of this, consider moving an endpoint of a hoizontal line. During planning, the horizontal line is presented with the message plan

horizline point1 moveby: delta

This message plan represents the actual request that might be made of the line at run-line. The horizontal line constructs a Smalltalk method for receiving a message that moves its point1, while still keeping istself horizontal. A selector is chosen for this method, say point1Moveby. Finally, the horizontal line returns a new message plan that provides directions for invoking this method, namely

Horizline point1Moveby: delta.

It is important to remember that a message is request to an object, not an operator that can freely manipulate the object that receives it. Thus, if an object is asked to transform a message plan, one of the things it can do it to indicate that it will refuse to receive such message. In this case, either the sender of the rejected message plan is notified, or if no provision was made for this, the Smalltalk error handler is called.

A more detailed example of transforming a message plan will now be given. The following classes will be used in this example:

Class Line

The object used in the example will be an instance r of DemoRectangle (Figure 5.5). [The class DemoRectangle is not the same as the normal Smalltalk class Rectangle, which has as its parts an upper-left hand corner and a lower right-hand corner. Constraint satisfaction would be trivial for instances of Rectangle.]

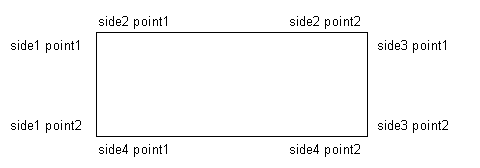
Figure5.5 – An instance of DemoRectangle

Suppose that the user wishes to pick up and move the right-hand side of r with the cursor. In the ThingLab window, this is accomplished by repeatedly asking r to move ist side by some increment delta, where delta is a point. [Strictly speaking, delta ought to be an instance of PointIncrement or some such class, rather than Point.] First, a message plan m is constructed and presented to r. This plan is:

r side3 moveby: delta

Here, the receiver is r, the path is side3, the action is moveby:, and the symbolic argument is delta. The rectangle is asked to transform m into a new message plan that gives directions for invoking a method for moving side3, while also satisfying all the rectangle’s constraints. Once a transform of m has been found, the window can use this information in moving the side.

The steps in transforming a message plan are outlined below. In the following sections, each of these steps is described in more detail.

First see if a transform of the message plan has already been constructed. If so, use it.

If not:

When r is asked to transform the message plan m, it first checks in its dictionary of transforms to see if such a transform has already been constructed. This dictionary consists on the name side of incoming message plans, and on the value side of transforms of these plans. In this case, suppose a transform for m is not in the dictionary.

If the prototype DemoRectangle were edited by adding or deleting parts, or its constraints or merges were changed, some of the transforms might become obsolete. Currently, all transforms are forgotten when any such change occurs. An improvement would be to check which ones are affected by the change, and to forget only these entries. [This would amount to keeping track of dependencies on a class-wide basis.]

The first name on the path of the message plan is side3. If r had no constraints or merges involving side3, then the transform would be constructed using a transform obtained from VerticalLine as a "subroutine". However, r does have merges involving side3, so this cannot be done. An example of using the transform obtained from a part will be presented later in this chapter.

The next step is to check if the message plan has a compile-time expansion. A message queue is created, and r asks its part, pointed to by the path side3, to expand the original plan into this queue. The vertical line uses the default expansion method inherited form Object, and expands the moveby: message plan into two moveby: message plans,one for each of its endpoints. The endpoints are in turn asked to do a compile-time expansion of These message plans. Points, however, are themselves willing to receive moveby: message at run-time, and the expansion stops. The message queue is now:

MessageQueue

More information about compile-time expansion may be found in the Leftovers section.

Each message plan in the queue is checked to see if its path overlaps the paths of any of the receiver’s constraints or merges. If a constraint overlaps a message plan, the copies of the constraint’s message plans are added to the queue. On the other hand, if a merge overlaps one of the message plans, the message plan is checked for each distinct path to the merged part.

The rectangle itself has no constraints. However, two of its merges do overlap the message plans in the queue. The paths side3 point1 and side2 point2 both refer to the same point. Therefore, the first message plan will be checked using both of these paths. The other message plan is treated in an analogous fashion.

Each message plan in the queue must now be checked against the constraints and merges of r’s parts. The first message plan with the first of its merged paths is

side3 point1 moveby: delta.

The first name on the path is stripped off, and the message plan

point1 moveby: delta

is forwarded to side3. This part is a vertical line, and its constraint overlaps the path of the forwarded message plan. Consequently, copies of the message plans that describe the methods this constraint can use to satisfy itself are added to the queue. The queue is now:

MessageQueue

Message plan 3 describes one of the methods for satisfying the vertical line’s constraint, namely the method

vert-point1-x

Message plan 4 describes the other method. Note that the paths of the contraint’s message plans have been prefixed by the name side3, since these messages are now for r.

The vertical line side3 strips off the next name on the path of message plan1, and forwards the message plan

moveby: delta

to its first endpoint. The point has no constraints or merges of its own. The plan’s path is now empty, and so there are no more subparts to be checked.

The other path to the upper right-hand corner, namely side2 point2, is now checked. This causes the constraint on the top horizontal line to add message plans 5 and 6.

MessageQueue

The other moveby: message plan is treated in a similar fashion. The message plans added by the constraints are checked as well, since they might overlap some other contraint or merge. There is a mechanism for preventing infinite recursion: before adding copies of its message plans a constraint checks to see if it has already added copies to the queue. If so, no new copies are added.

The final state of the queue is:

MessageQueue

Message plans 3 and 4 were added by the vertical constraint on side3, message plans 5 and 6 by the horizontal constraint on side2, and message plans 7 and 8 by the horizontal constraint on side4. None of the varios paths of the message plans in the queue overlap the vertical constraint on side1, and so that constraint added no plans.

The first step in processing the message plans is to look for preferences. The system distinguishes preferences form relations that must hold. Requests made by the user to change a value are considered preferences: the system will attempt to honor them, but if the request violates a constraint, it will be overridden. Message plans 1 and 2, which represent the user’s request to move a side, are preferences of this sort. The message described by these plans will be sent first. The system will attempt no to undo these edits, but may do so if pressed. After processing the preferences, message plans 1 and 2 are removed from the queue, and put in the list of plans describing messages to be sent first. Also, the constraint satisfier notes that the point that these message plans affect should not be changed unless necessary.

Messages to be Sent First

Propagation of degrees of freedom is used next. In using this method, the constraint satisfier look for a message plan such that its target has enough degrees of freedom to satisfy all its constraints. Its turns out that all six remaining message plans meet this requirement, since each of the numbers that are their targets has only one constraints that affects it. Thus, any of these numbers could be chosen so as to satisfy its constraint. However, the constraint satisfier would prefer not to alter side3 point1 or side3 point2. The constraint satisfier notes that, after taking merges into account, these two paths overlaps all the message plan’s paths except for those of message plans 5 and 7. The constraint satisfier the decides that the messages described by these two plans can be sent last.

Since these messages will take care of satisfying the two horizontal constraints, the remaining two message plans added by the horizontal constraints can be discarded.

Message to be Sent First

[Incidentally, if the system were running on a multi-processor machine, the constraint satisfier could have included as part of the plan the information that messages 5 and 7 could be sent in parallel. See Chapter 6.]

Propagation of degrees of freedom is tried again. This time, the only message plans remaining do affect side3. So the constraint satisfier decides to send the message described by one of these plans, say message plan 3. [The contraint satisfier is not smart enough to realize that if the vertical constraint were satisfied before moving the line, it would be satisfied after the entire line is moved. Thus, the message described by plan 3 will actually be sent, even thought if won’t change anything.] Sending this message will take care of satisfying the vertical line constraint, so message plan 4 may be discarded. The queue is now empty, and this phase of constraint satisfaction is over.

Message to be Sent First

A plan has been constructed for moving side3 while still satisfying all the rectangle’s constraints. The systeem now embeds this plan in a Smalltalk method understood by DemoRectangle. A name for this method is generated by ingloriously squishing together the path and action from the message plan. Code for the method is accumulated by asking each of the message plans to add code to a stream. The method compiled by the system is:

side3Moveby: delta

At run-time, this method will in turn invoke methods belonging to the horizontal and vertical constraints, namely

Class HorizontalLine

The rectangle r is now able to return a transform of the original message plan

Side3 moveby: delta.

The transform is simply

Side3Moveby: delta.

In other words, the transform has an empty path, and its action is to invoke the newly compiled method. The message-transform pair is indexed in DemoRectangle’s dictionary of transforms. At this point, the reader who has waded through all the steps will appreciate the virtues of saving this transform for future use.

Parts of the transformation process not exercised by the above example will now be described.

In the last section, it was mentioned that in the absence of interactions with the receiver’s constraints, the transform obtained from a part could be used as a "subroutine". Consider an object consisting simply of two rectangles.

Class TwoBoxes

Suppose that the user wants to move the right-hand side of box2. The instance of TwoBoxes is asked to transform a message plan m, namely

box2 side3 moveby: delta.

Furter, suppose that there is no entry for m in TwoBoxes’ dictionary of transforms. The next step is to check the first name on m’s path for interactions with TwoBoxes’ parts. The first name is box2. There are no constraints or merges involving box2 (in fact there are none at all). Therefore, the transform obtained from DemoRectangle may be used. TwoBoxes strips the first name off m’s path, and asks DemoRectangle to transform the message plan

side3 moveby: delta.

DemoRectangle looks up this plan in its dictionary, and Quickly returns the transform

Side3Moveby: delta.

TwoBoxes inserts the name box2 at the head of the path, and returns as its transform

box2 side3Moveby: delta.

Another way of describing this process is that when there is no interference, plans obtained from an object’s parts are re-used. The result of this is that plans for receiving a message are stored as far down in the part-whole hierarchy as possible. There are much more powerful ways in which the idea of plans obtained from subparts could be used. See Chapter 6.

Compile-time expansion is used with message plans that describe such things as translation and scaling. Most message plans, however, simply expand to themselves.

There are two reasons for using the technique of compile-time expansion. First, it is not easy to write, say, an efficient but general moveby: message. A first cut might be to have a default moveby: message that simply asked each part to move, with points overriding the default. This handles such things as lines, but fails in general. Consider a triangle.

Class Triangle

If the triangle received a moveby: message, it would in turn ask each of its sides to move. Each side would then ask its endpoints to move. But because of the merges, each vertex would be moved twice! It would be possible to keep track at run-time of all the objects that have already been moved. However, by using compile-time expansion, this can all be done during planning. The original moveby: message plan would be expanded to:

MessageQueue

The system then notices which of the message plans refer to the same object, and eliminates the duplicates. The following code would be compiled for Triangle:

One way of looking at the process of eliminating duplicate message plans is to notice that the duplications arise because of merges. Merges are just an efficient way of representing an equality constraint. If the merged parts had not actually been collapsed internally, there would have been an appropriate number of messages to each part.

The benefits of doing compile-time expansion during planning are greater with more complex message plans. Another message plan that undergoes compile-time expansion is the "move the i-th attacher" message. (See Chapter 2 for examples of attachers.) The expansion here is

fix the locations of attachers 1 to i-1, and move attachers i to n

This message is used when inserting a new part into object being edited. For example, suppose the three vertices of an instance of Triangle have been designated as attachers. When inserting a triangle, the user positions the first vertex (with the entire triangle following), then the second vertex (moving the second and third vertices), and then the third vertex. During planning the message plan

moveAttacher: 2 by: delta

is expanded to:

MessageQueue

[Note: the message fix means "add this path to Unalterable, but don’t generate any code".] Again, all this could be done at run-time, but much less efficiently.

The other reason for using compile-time expansion is that it is a way to avoid waking up constraints needlessly. For example, consider the voltage divider again. Suppose the user wants to move r1. This involves asking the voltage divider to transform the message plan

r1 moveby: delta.

Using the constraint satisfaction scheme described above, but without compile-time expansion, any constraint overlapping the path r1 would add message plans to the queue. In other words, r1’s electical as well as graphical constraints would need to be checked. With compile-time expansion, the plan is expanded to

r1 lead1 node location moveby: delta

and only the graphical constraints on r1 are checked.

In the above examples, the user’s desires could be completely met, and all the object’s constraints satisfied as well. This is not always possible. Consider a horizontal line with one end anchored. If the user tries to move the other end with the cursor, the moving end will in general not be able to follow the cursor exactly – the x value of the endpoint will match that of the cursor, but the y value will remain constant (see Figure 5.6).

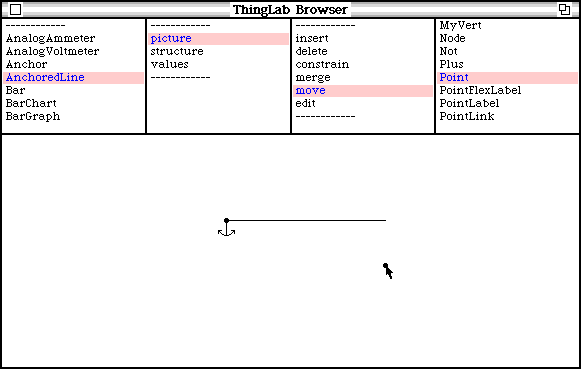
Figure 5.6 – An anchored horizontal line

The classes for this example are as follows.

Class HorizontalLine

The compiled method for moving point2 of an instance of AnchoredLine is:

AnchoredLine

In other words, the anchored line will first make the change to its points2, but will partailly undo it to satisfy its constraint.

The last section of this chapter moves up from detailed discussion of constraint satisfaction to a more general level.

Several years ago, a major debate in artificial intelligence circles was occurring between advocates of procedural and declarative representations of knowledge. Although indulgence in this debate is no longer as fashionable as it once was [‘Anyone who hasn’t figured this ‘controversy’ out yet should be considered to have missed his chance, and be banned form talking about it." McDermott 76], the issues raised by it still remain. It is interesting to view the current ThingLab constraint mechanism and its evolution in the light of this debate.

Superficially, the debate is between researchers who want to embed the knowledge that a system has in its procedures, and researchers who want to represent knowledge as a set of facts together with general-purpose programs for manipulating these facts. On the procedural side, an extreme on the declarative side is a system that represents all its knowledge in first-order predicate calculus and uses a resolution theorem prover to manipulate these facts.

Constraints are an amalgam of both declarative and procedural information. On the declarative side, a constraint states what the relation is, which subparts of the object are affected by the constraint, and which subparts may be altered to satisfy it. On the procedural side, it describes procedures for making that relation be true. Notice, however, that the procedural parts of the constraint are rather tightly controlled. These methods are invoked by the system, not the programmer, Each of the methods, if invoked, must cause the constraint to be satisfied. The side effects of the methods are described by message plans: each plan has a path to the part of the constraint’s owner that the method alters; the method may alter no other parts. There is also relationship that must hold among the constraint’s methods. For every part that is referenced by one of the methods, there must either be another method that alters it, or a dummy method referencing it.

In this essay Frame Representations and the Declarative/Procedural Controversy [Winograd 1975], Terry Winograd writes

Viewed in this light, the constraint mechanism is more than the result of simply pasting together facilities for representing facts and procedures. An individual constraint provides a way of integrating the declarative description of a relation with procedures for achieving it, and is thus a more powerful tool than a simple statement of a fact. More globally, constraints achieve the same sort of modularity as declarative systems, in which each fact can be stated independently. Indeed, it is in the area of interaction that the current constraint mechanism falls down. Within it, one cannot represent such things as the making off of a constraint, or a suggestion as to how to satisfy a set of constraints.

One can view the evolution of the constraint mechanism in ThingLab as starting with a rather strictly declarative representation, and moving toward the inclusion of more procedural sorts of knowledge – richer ways of describing the interaction of a constraint with its environment. In the first implementations, constraints were represented using only an error expression, and relaxation was the only means of satisfying them. In contrast the current system attempts to use the local procedures provided by the constraint for statisfying itself. Some further steps in this evolution are proposed in Chapter 6, such as constraints involving time, and meta-constraints.